Comprendre la descente de gradient en 3 étapes et 12 dessins

Tout le monde a déjà entendu parler de l’algorithme de descente de gradient, mais… savez-vous vraiment comment ça marche et l’avez-vous déjà implémenté par vous-même pour être sûr d’avoir bien compris comment ça marche ?

Utiliser des modules qui font les calculs pour nous, c’est cool.

Comprendre ce qu’on manipule, c’est mieux !

C’est ce qu’on va faire dans cet article, en trois étapes :

1. La descente de gradient, qu’est-ce que c’est ?
2. Comment ça marche ?
3. Et quels sont les pièges à éviter ?

Les seuls pré-requis à cet article sont de savoir ce qu’est une dérivée.

C’est parti !

C’est quoi la descente de gradient ?

Il s’agit d’un algorithme permettant de trouver le minimum d’une fonction.

C’est une problématique qu’on retrouve partout en mathématiques.

Et en data science, c’est aussi le cas, surtout quand on veut trouver l’estimateur du maximum de vraisemblance.

Ce qu’on fait tout le temps.

Ah oui, et trouver un minimum, c’est la même chose que trouver un maximum, il suffit juste de changer le signe.

Quand on est au lycée, pour trouver le minimum d’une fonction, on fait autrement, on :

• Calcule la dérivée première.
• On résout l’équation dérivée égale à 0 pour trouver les points d’inflexion.
• On calcule la dérivée seconde en ces points. Quand elle est positive, c’est un minimum. Quand elle est négative, c’est un maximum.

Ok, cool, ça c’est une technique qui marche bien.

SAUF…

…quand on manipule des expressions tellement compliquées que ça devient impossible à résoudre.

Typiquement quand on fait du machine learning ou du deep learning.

La descente de gradient offre une approche :

• algorithmique
• itérative
• qui marche plutôt bien dans la plupart des cas

Je rajoute ce dernier point parce que parfois on a des problèmes avec cet algorithme, mais il existe des extensions pour résoudre ces problèmes.

n ne s’attardera pas trop là-dessus dans cet article mais on verra quand même les problèmes les plus classiques.

Comment ça marche ?

Je vais d’abord vous donner une explication un peu intuitive, et ensuite on fera des maths.

Imaginez que vous soyez un skieur dans la montagne.

Et vous voulez trouver le point le plus bas (c’est-à-dire trouver le point à l’altitude minimale).

Votre approche, ça va être de vous mettre face à la pente (descendante), et boom vous avancez dans cette direction pendant 5 minutes.

5 minutes plus tard, vous êtes à un nouveau point.

De nouveau, vous vous mettez face à la pente et avancez dans cette direction pendant 5 minutes.

Et ainsi de suite..

Et au bout d’un moment, à force de toujours descendre, vous arriverez tout en bas.

Facile !

Comment ça marche mathématiquement ?

En maths, la pente, ça correspond à la dérivée :

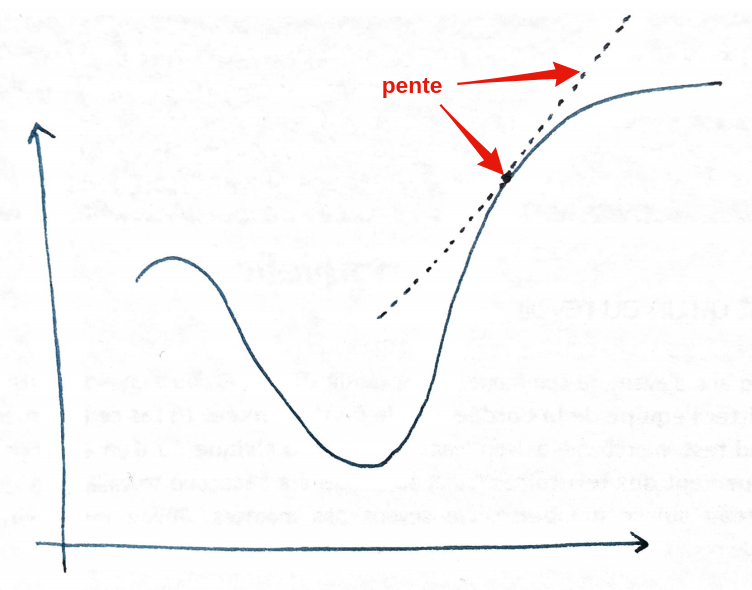
La valeur de la dérivée correspond à l’inclinaison de la pente en un point donné.

Donc :

• si la dérivée est élevée, c’est que la pente est très pentue.
• Et si la dérivée est faible, la pente est faible.
• Si la dérivée est égale à 0, c’est tout plat. C’est le cas au minimum par exemple.
• Et si la dérivée est négative, c’est que ça descend (quand on va vers la droite !).

Donc une fois qu’on a la valeur de la pente, comment est-ce qu’on fait pour descendre ?

On va à l’inverse de la pente !

• Dérivée positive => pente qui monte vers la droite => on va vers la gauche.
• Dérivée négative => pente qui descend vers la droite => on va vers la droite.

Ok, alors sur le dessin, on a compris qu’il fallait aller vers la gauche.

Mais de combien ?

Est-ce qu’on fait un seul pas, deux pas, on continue pendant combien de temps ?

En fait, on aimerait bien faire juste un pas, se reposer la question de la dérivée, puis refaire un pas, etc.

Sauf que ça va être très gourmand en calcul (on va prendre beaucoup de décisions) si on fait ça. Et donc ça va être lent.

Mais d’un autre côté, si on fait des gros pas, on risque de louper le minimum, donc revenir dans l’autre sens, re-dépasser le minimum, et ainsi de suite, sans jamais tomber dessus.

Il faut juste trouver le juste milieu !

Ça se fait en spécifiant ce qu’on appelle un taux d’apprentissage. On va en reparler un peu plus tard.

Et les maths, dans tout ça ?

Prenons un exemple, et arrêtons avec les dessins moches à la main.

Considérons la fonction suivante :

\[f(x) = 2x^2 \cos(x) - 5x\]

import numpy as np
def f(x):
    return 2 * x * x * np.cos(x) - 5 * x

Et étudions-la sur l’intervalle \([-5, 5]\) :

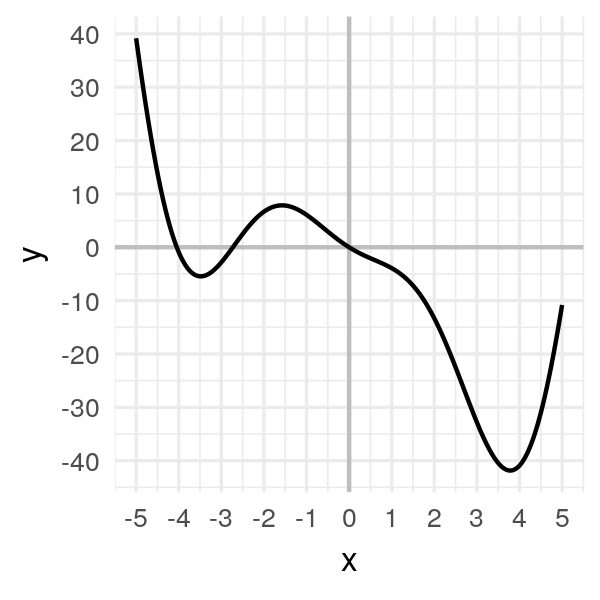
L’objectif est de trouver le minimum qu’on voit à droite, vers x entre 3 et 4.

On pourrait, dans ce cas, faire le calcul de la dérivée égale à 0, mais le but c’est de comprendre la descente du gradient, donc c’est ce qu’on va faire.

Il y a 3 étapes :

1. On prend un point au pif \(x_0\).
2. On calcule la valeur de la pente \(f'(x_0)\).
3. On avance dans la direction opposée à la pente : \(x_1 = x_0 - \alpha * f'(x_0)\). Ici, \(\alpha\) correspond à ce fameux taux d’apprentissage, et le moins permet d’aller dans la direction opposée.

Première étape : On prend un point au pif \(x_0 = -1\). Ce qui correspond à \(f(x_0) = 6.08\).

x = [-1.]
f(x[0])
# 6.08060

Dessinons une grosse boule à cet endroit-là :

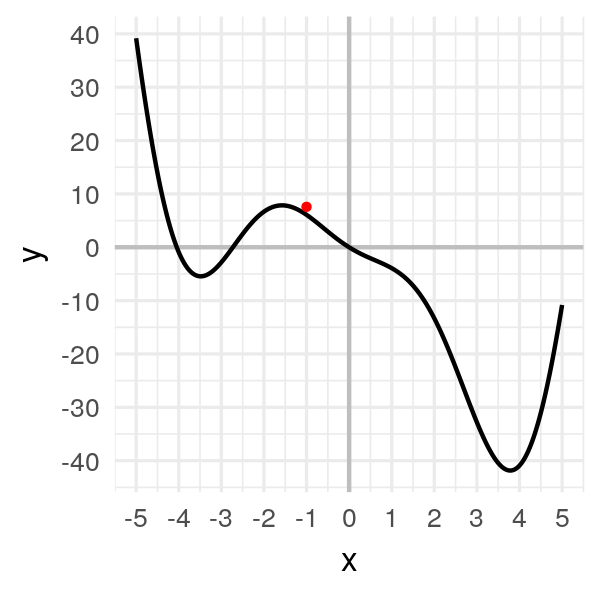
Deuxième étape : On calcule la valeur de la pente.

def df(x):
    return 4 * x * np.cos(x) - 2 * x * x * np.sin(x) - 5

slope = df(x[0])
slope
# -5.47827

On a donc une pente négative égale à \(-5.23913\).

Troisième étape : On avance dans la direction opposée à la pente : \(x_1 = x_0 - \alpha * f'(x_0)\).

Comment choisir la valeur de \(\alpha\) ?

Je propose pour le moment de tester une petite valeur \(\alpha = 0.05\), et on testera d’autres valeurs un peu plus tard.

alpha = 0.05

x.append(x[0] - alpha * slope)
x[1]
# -0.72609

On a notre nouvelle valeur pour notre point ! Affichons-le :

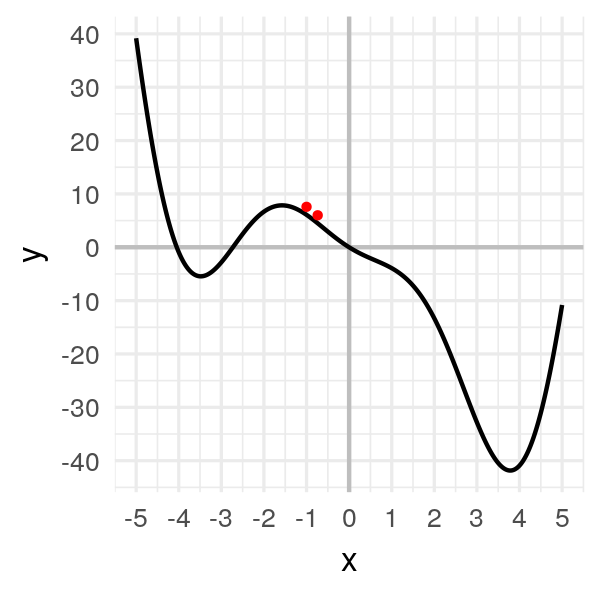
On a bougé d’un tout petit peu.

Cette approche est itérative, ça veut dire qu’il va falloir répéter plusieurs fois l’opération pour arriver au minimum.

Recommençons :

x.append(x[1] - alpha * df(x[1]))
x[2]
# -0.40250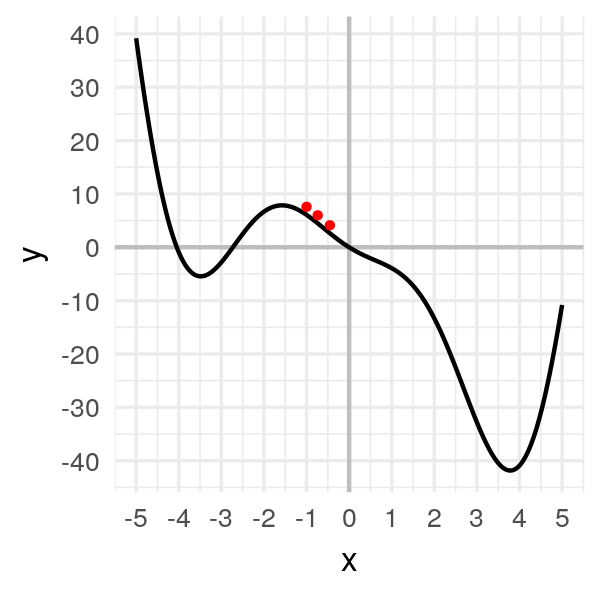

On avance doucement.

Après un peu plus d’une dizaine d’itérations, notre algorithme converge :

x = [-1.]
for i in range(20):
    x.append(x[i] - alpha * df(x[i]))
x
# [-1.0, -0.7260866373071617, -0.4024997370140509, -0.08477906213634434, 
# 0.18205499002642517, 0.39684580640116923, 0.5797318757542436, 
# 0.7511409760238664, 0.929843593497496, 1.1379425635322518, 
# 1.4100262396071885, 1.8111367982460322, 2.4659523010837896, 
# 3.481091120446543, 3.9840239754024296, 3.5799142362878964, 
# 3.9342838641256046, 3.6341484369757358, 3.900044342976242, 
# 3.670089111844099, 3.8747793435314155]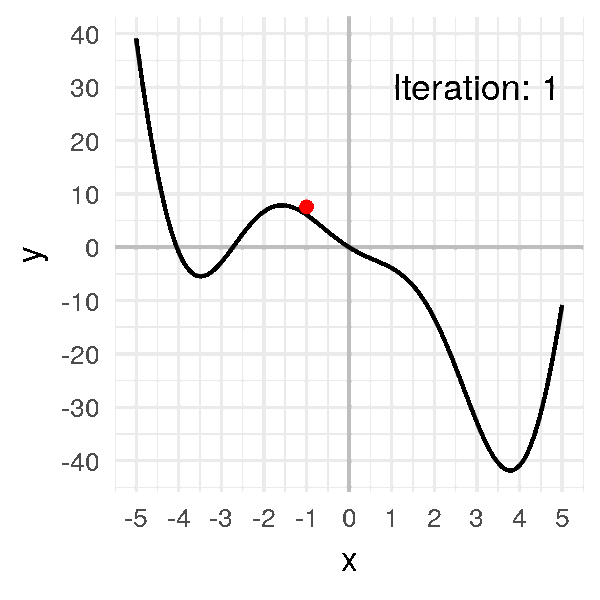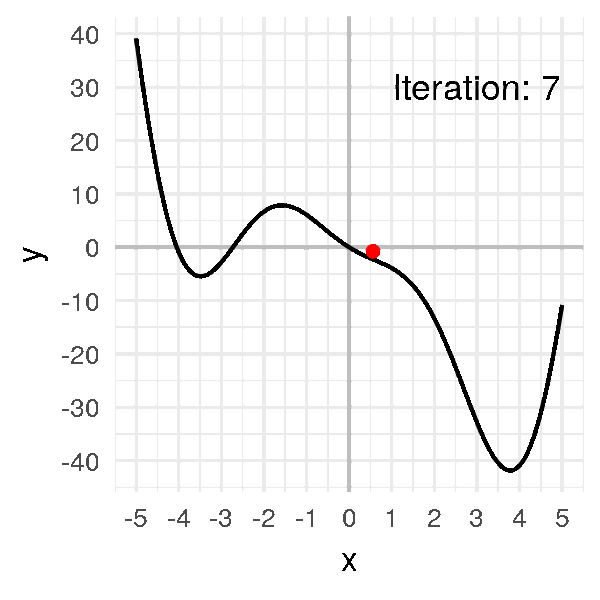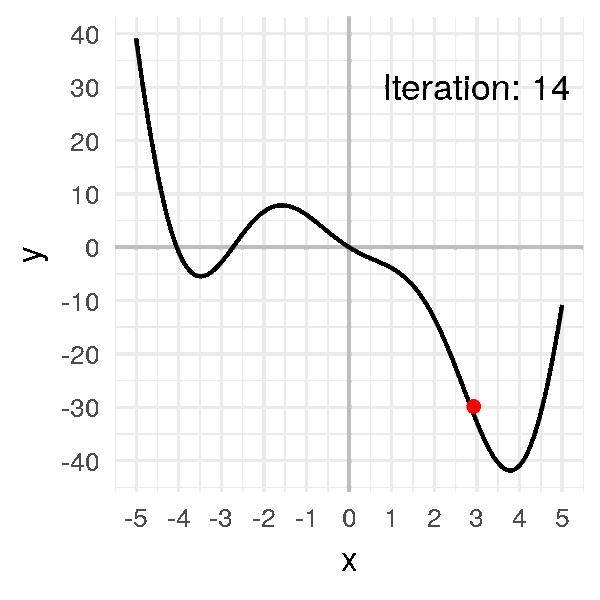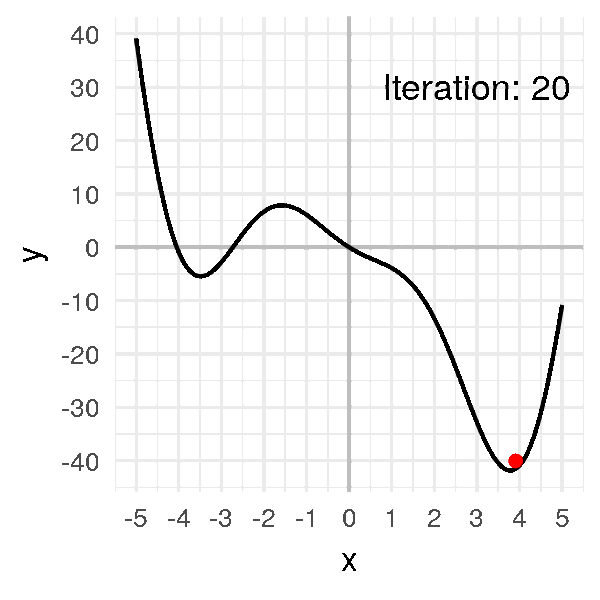

Notre petite boule finit par arriver au minimum et à y rester, à environ \(x = 3.8\).

Les pièges à éviter

Bon.

Là, on a vu le principe de la descente de gradient.

Sur un exemple simple.

Mais en vrai il arrive souvent qu’on rencontre des problèmes. Par exemple :

• Comment fixer le taux d’apprentissage ?
• Comment régler le problème du vanishing gradient ?
• Comment lutter contre les minima locaux ?

C’est ce qu’on va voir tout de suite !

Comment fixer le taux d’apprentissage ?

Dans l’exemple précédent, on s’est fixé \(\alpha = 0.05\).

Pourquoi ?

J’ai un peu triché.

J’ai testé avant et j’ai vu que c’était une valeur qui marchait bien.

En fait, il faut trouver le juste milieu en prenant en compte que :

• Plus la valeur \(\alpha\) est grande, plus on va avancer vite, mais l’algorithme risque de ne jamais converger.
• Plus la valeur \(\alpha\) est petite, plus on va avancer lentement, et donc plus ça va être long de converger.

Par exemple, avec une valeur \(\alpha = 0.2\), on obtient :

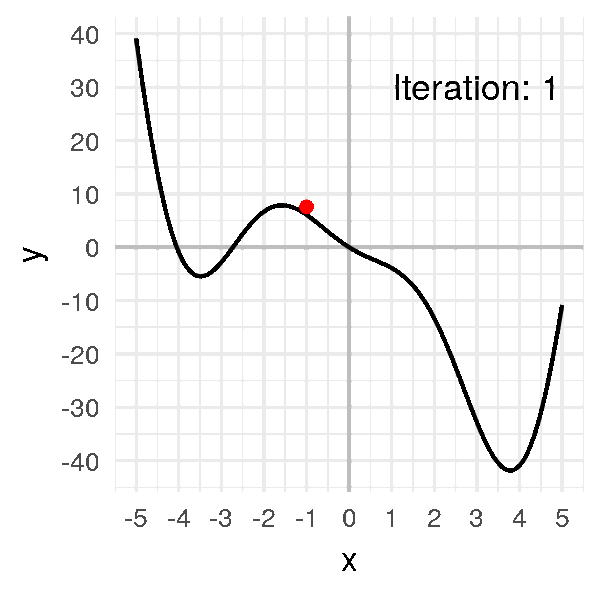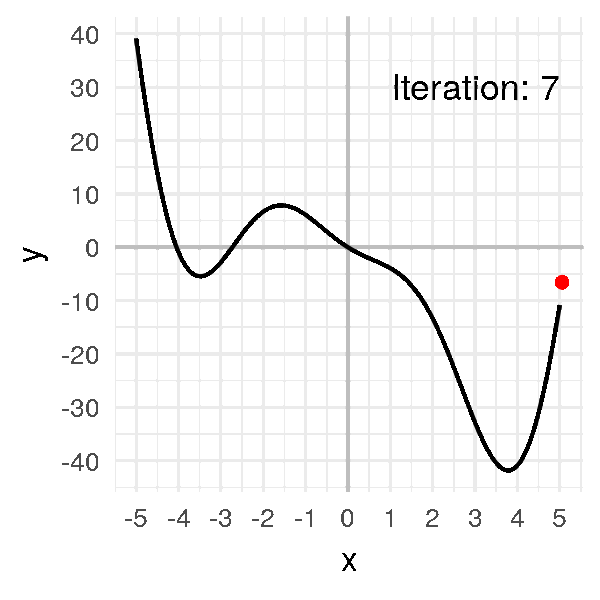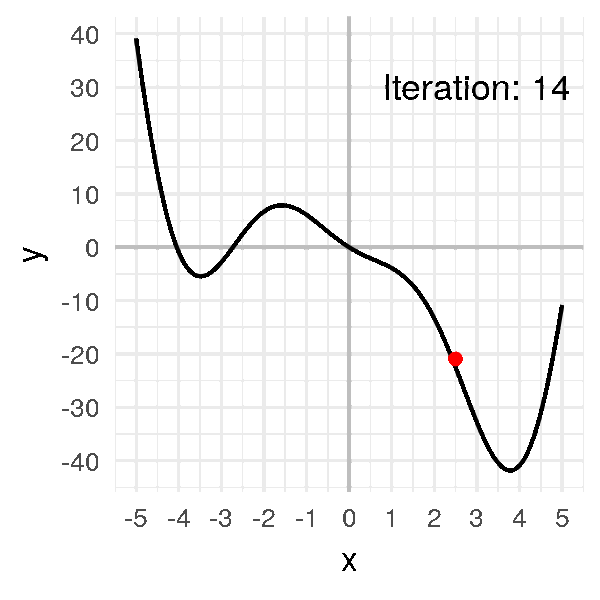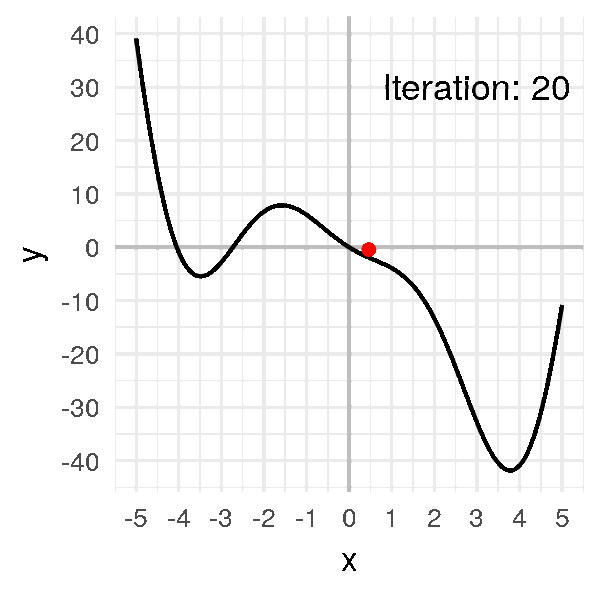
Là on voit qu’on a un problème de convergence. La valeur \(\alpha\) est trop grande.

Du coup, quand le skieur est face à la pente, il avance tellement qu’il se retrouve de l’autre côté de la montagne.

Si on prend une valeur trop petite, comme \(\alpha = 0.001\) :

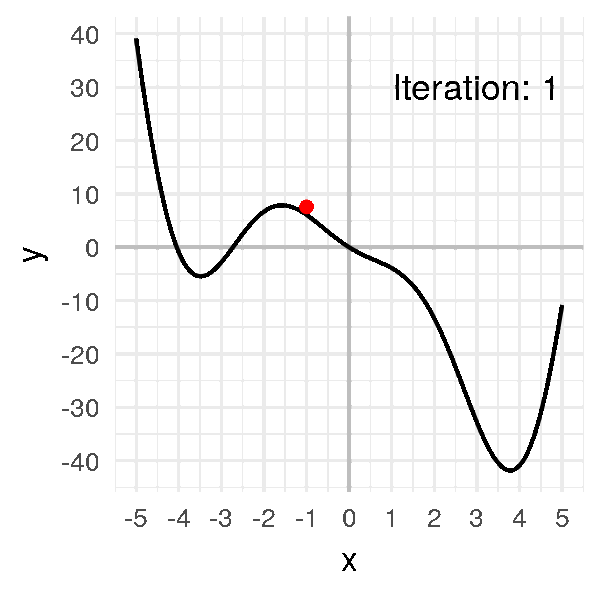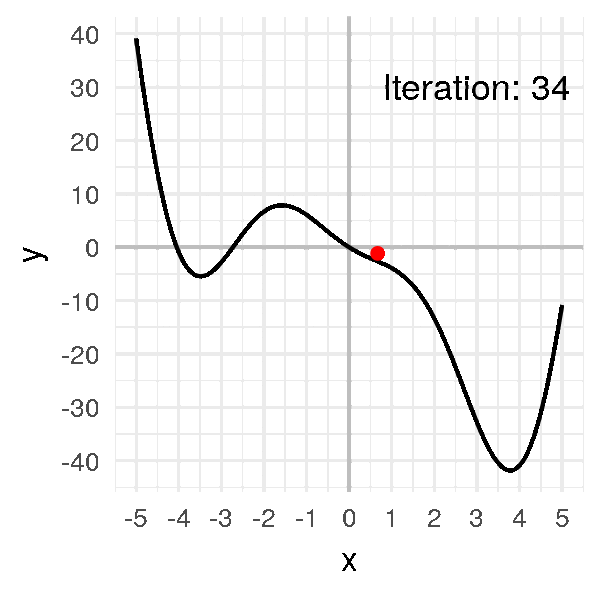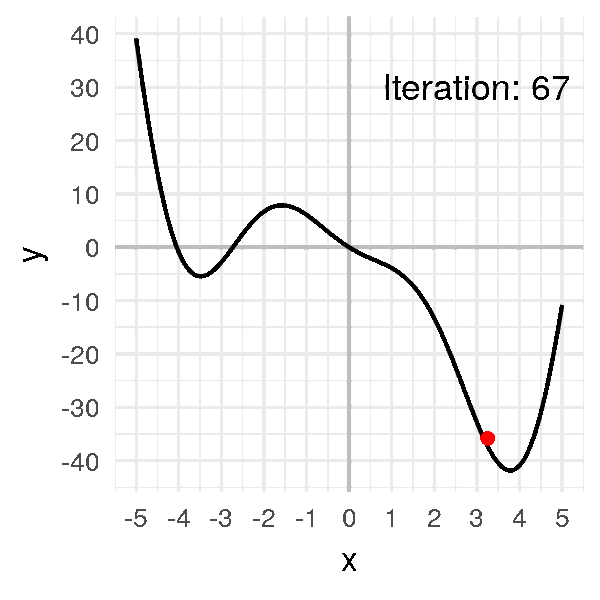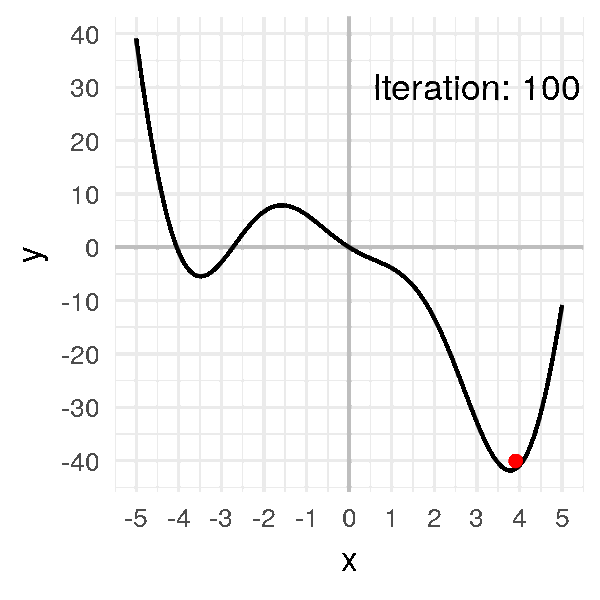
Ça marche, ça converge, sauf que ça prend beaucoup plus de temps !

J’ai dû accélérer l’animation, puisque cette fois-ci, au lieu d’arriver au minimum en 15 itérations, ça prend cette fois-ci 75 itérations, soit 5 fois plus de temps !

Pour notre problème simple, l’impact est faible, mais quand on entraîne des réseaux de neurones, ça fait une grosse différence en temps de calcul !

Malheureusement, il n’y a pas de recette miracle pour trouver le taux d’apprentissage parfait.

Pour le trouver, il faut en tester plusieurs et prendre le meilleur.

Comment régler le problème du *vanishing gradient* ?

Il existe deux problèmes très récurrents en Deep Learning, le exploding gradient et le vanishing gradient.

Dans le premier cas, ça revient à avoir un taux d’apprentissage trop élevé qui va causer une instabilité de l’algorithme.

En Deep Learning, ça peut arriver quand on a un très gros réseau. Comme les gradients de chaque couche sont multipliés entre eux, on peut très rapidement avoir un gradient qui explose de manière exponentielle.

Pour le vanishing gradient, c’est l’inverse.

Le gradient devient tellement petit que notre skieur n’avance quasiment plus. Ça peut arriver si le taux d’apprentissage est trop petit, comme on l’a vu.

Mais ça peut aussi arriver si notre skieur est coincé sur une sorte de plateau.

Imaginez la fonction suivante :

\[f(x) = \arctan(x^2)\]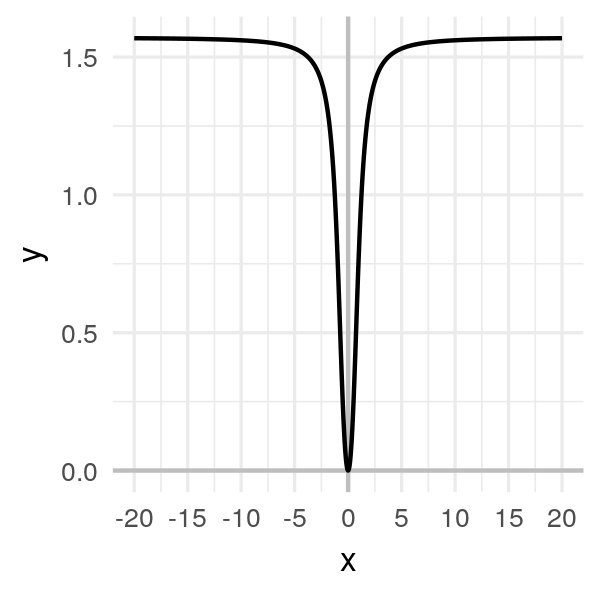

Clairement, le minimum est en \(x = 0\).

Supposons que le point au hasard tombe sur une valeur éloignée de \(0\), comme \(-20\).

Je choisis un taux d’apprentissage très élevé par rapport aux exemples précédents, à \(\alpha = 1\), et j’obtiens un algorithme trèèès long à converger :

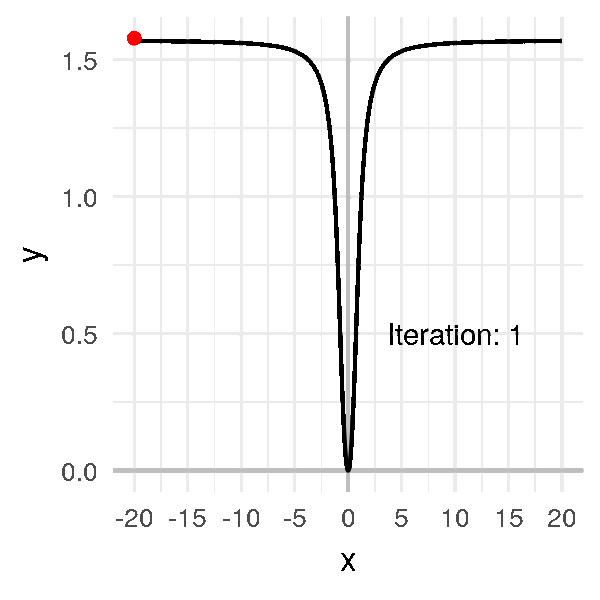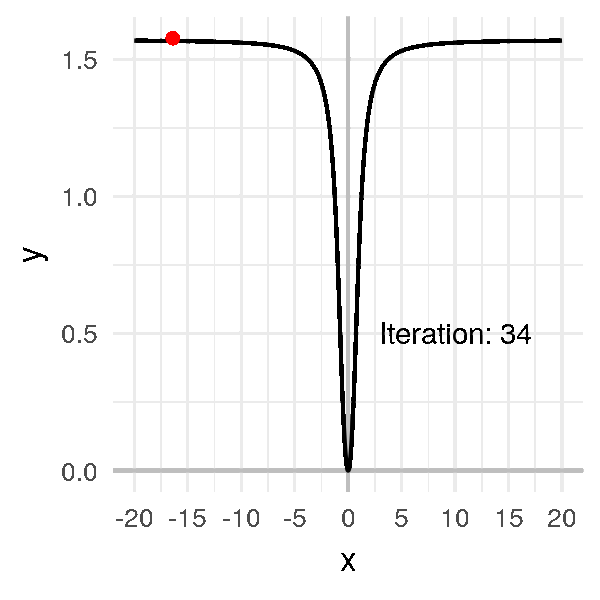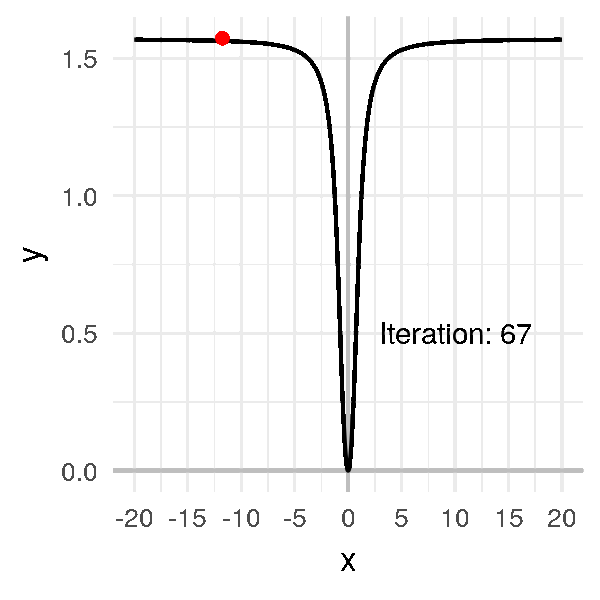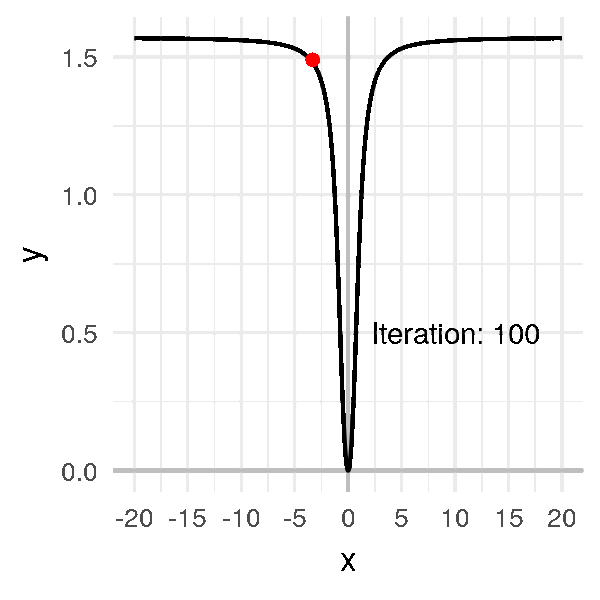
Là dans cet exemple on arrive quand même à trouver le minimum.

Mais imaginez une fonction plus complexe qui soit un mélange de celle-ci, avec un long plateau plat, et des montagnes russes à d’autres endroits.

À ce moment-là, quelque soit le taux d’apprentissage qu’on choisit, on aura des problèmes. Soit une très lente convergence, soit une instabilité de l’algorithme.

En Deep Learning, on résout ce type de problème avec les fonctions ReLU.

Comment lutter contre les minima locaux ?

Considérons cette fois-ci la fonction suivante :

\[f(x) = x \cos(x)\]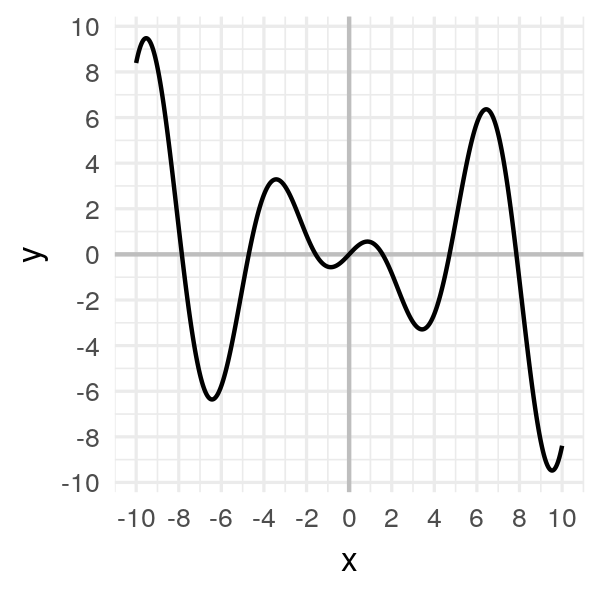

Le problème de cette fonction est qu’il y a beaucoup de minima locaux, c’est-à-dire des creux, qui ne sont pas le minimum global (qui, sur cet intervalle, se trouve à droite, autour de \(x = 9.5\))

L’animation suivante montre quelques exemples où je fais varier le point initial :

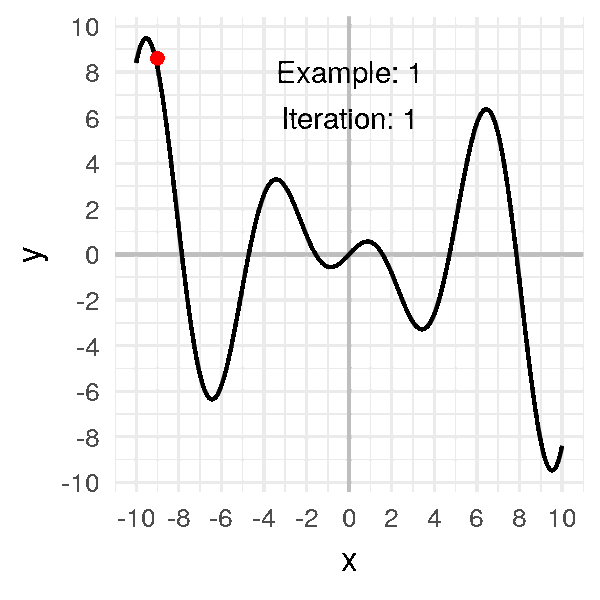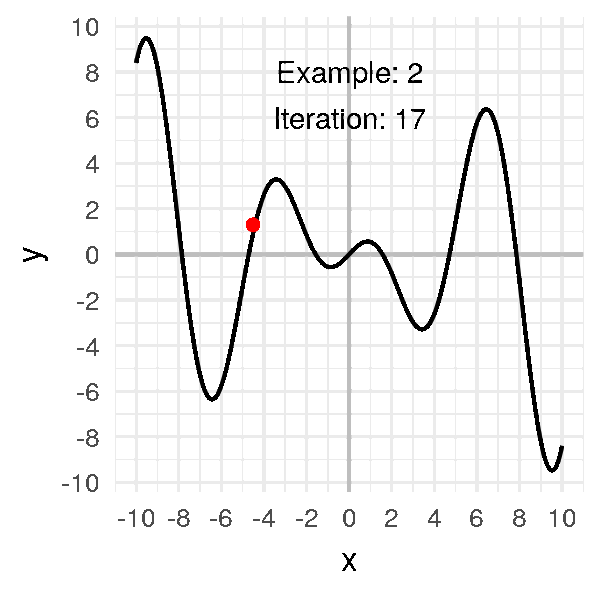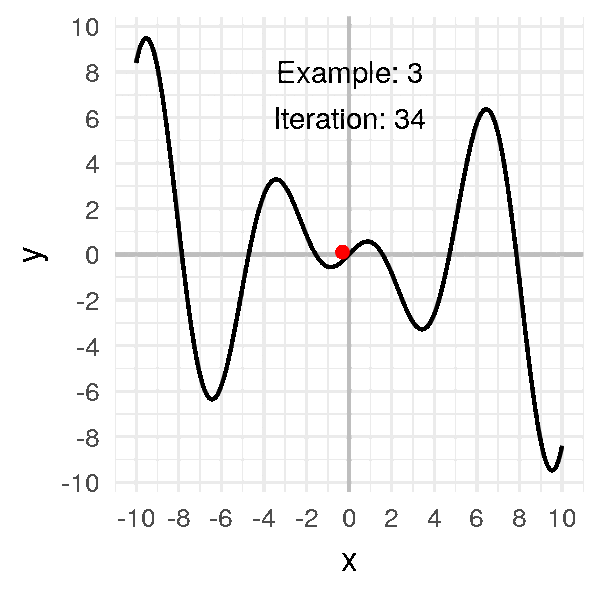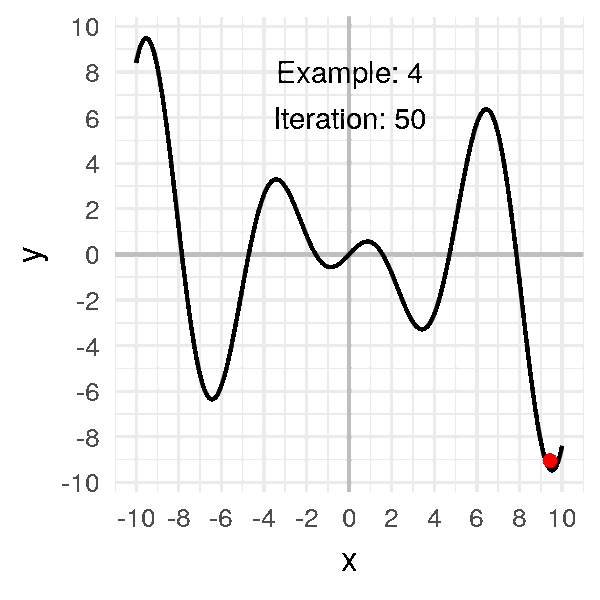
On s’aperçoit que le point de convergence dépend énormément du point initial.

Parfois il va arriver à trouver le minimum global, et d’autres fois, l’algorithme va rester coincé dans un minimum local.

Une technique pour éviter ce problème consiste justement à faire tourner l’algorithme plusieurs fois, et de garder le plus petit des minima, mais évidemment c’est plus gourmand en calculs.

Ensuite…

Dans cet article, vous avez appris :

• Ce qu’est la descente de gradient
• Comment est-ce que ça marche mathématiquement
• Et comment éviter les pièges les plus classiques

Si vous voulez aller plus loin, je vous invite à essayer par vous-même de l’implémenter sur un algorithme de Machine Learning. Par exemple, commencez avec la régression logistique !

C’est ce que je ferai dans un prochain article…